New methodologies in Geostatistics
Simulation of Gaussian fields on a Sphere
Different covariances lead to very different textures. In particular, the linear covariance creates anti-correlations which are evidenced by a day-night effect on the realization. These simulations on the sphere are used in particular to model climatological phenomena at the level of the terrestrial globe.
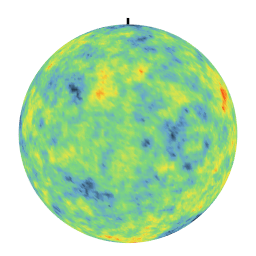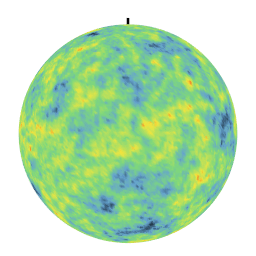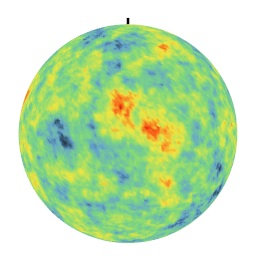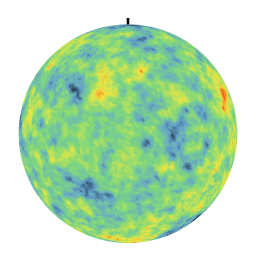 |  |
| Exponential Covariance | Linear Covariance over [0,pi] |
Geostatistics using SPDE approach
Many operational geostatistical issues are solved by using the fact that random functions can be seen as solutions of stochastic partial derivatives equations (SPDE). The numerical resolution of these equations (finite elements) opens the avenue to more efficient Geostatistics as it relies on sparse matrix algebra.
In addition, by varying the coefficients of the SPDE in space, this makes it possible to get rid of the stationarity assumptions concerning the structure parametrized (ex: variable anisotropy)
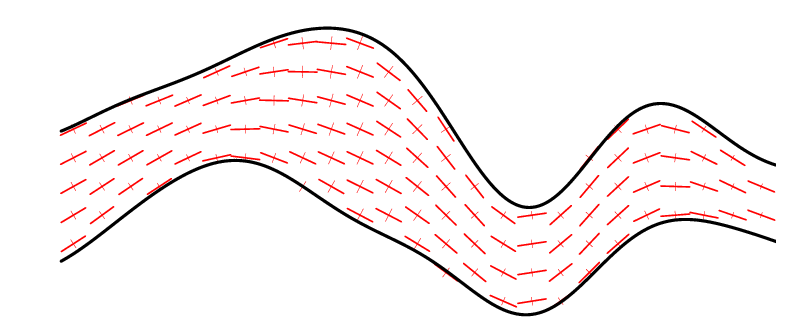 | 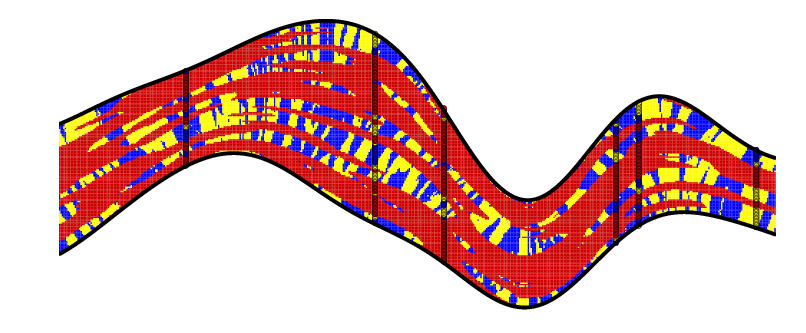 |
| Anisotropy which follows the geometry of the layer | Outcome of a PluriGaussian Random Function conditionned by Facies data along 5 vertical wells. |
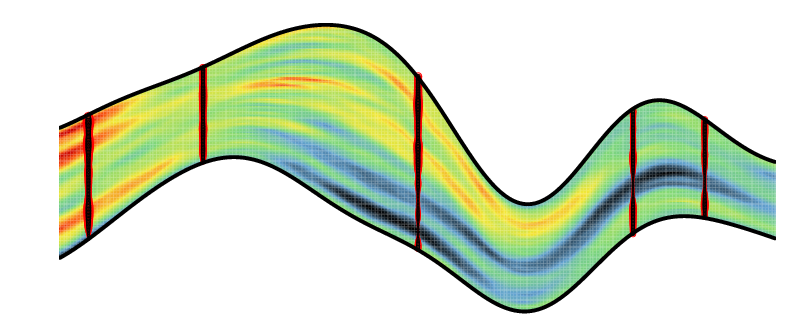 | 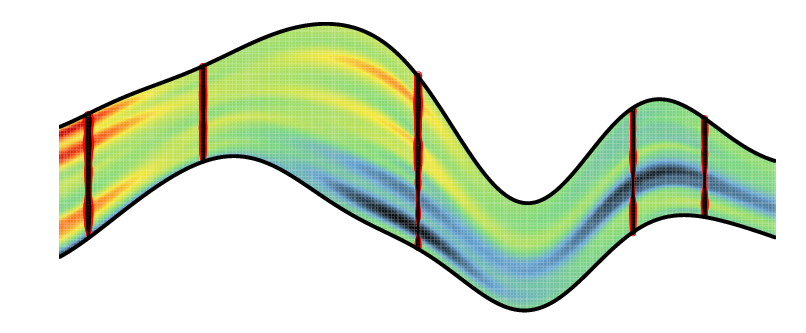 |
| Simulation of a Gaussian Random Function conditionned by data along 5 vertical wells. | Kriging estimate of Gaussian Random Function conditionned by data along 5 vertical wells |
SPDE model can take into account complex anisotropies, in particular in the case of non-unfoldable geometry (vortex example)
 | 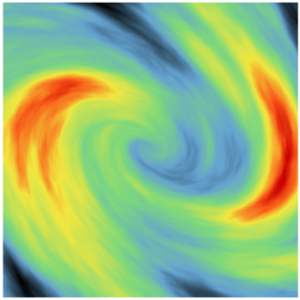 |
| Anisotropy field | SPDE simulation with complex anisotropy |
The extension to a regular Riemannian variety is immediate as soon as the corresponding meshing is available.
 |  |  |  |
| Gaussian Simulations | Truncated Gaussian Simulation | ||
Spatio-temporal SPDE Models
The SPDE approach is also available for modeling the spatio-temporal phenomena.
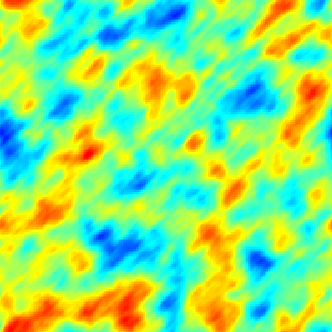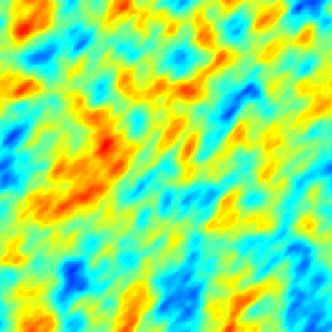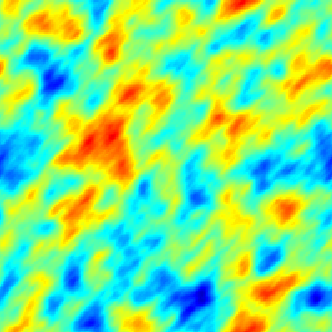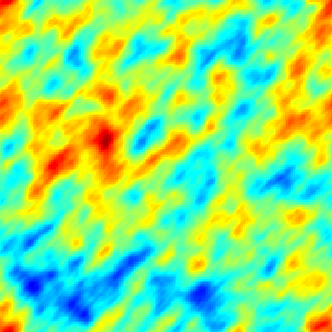 | 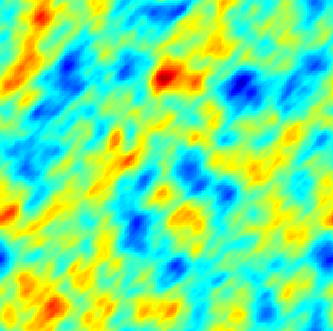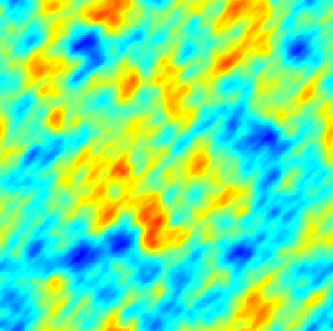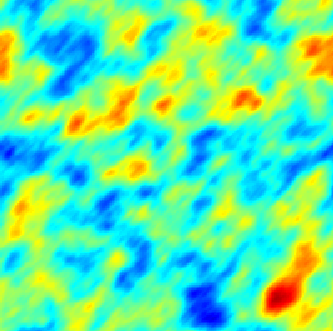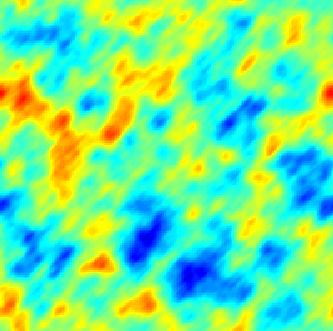 | 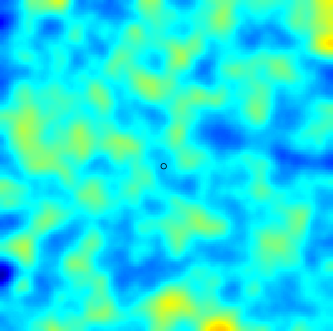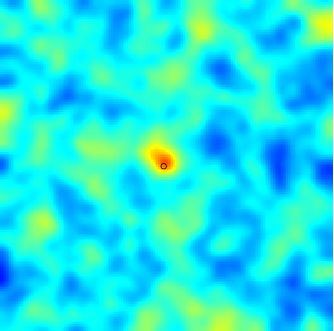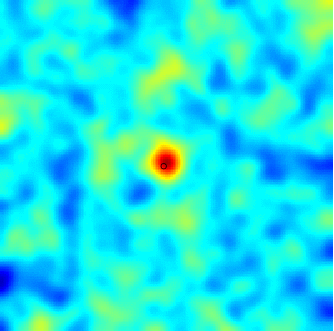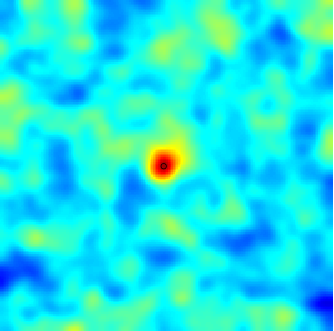 |
| Space-Time Separable Model | With advection | Diffusive Model with Source terms (deterministic + random) |
In the space-time framework, the SPDE approach makes it possible to integrate behaviors dictated by physical processes (diffusion, advection, ...) into geostatistical models.
Max-stable Model
Gaussian extremal random field: obtained as the maximum of Gaussian random fields (of given covariance) weighted by Poisson process arrival times. These models are able to represent spatial phenomena with extreme values. They are used to represent temperature or pluviometry fields in exceptional circumstances (ex: Cévennes rainfall episodes)
 | 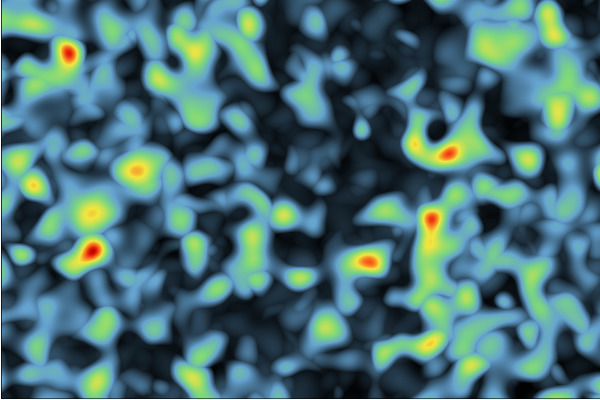 |
| Exponential Covariance | Gaussian Covariance |
Substitution Random Function Model
The Substitution Model is based on the combination of a spatial random function and a coding process. It allows producing simulations conditioned by facies data. This model has been successfully applied to reproduce the geometry and morphology of stromatolites in a study carried out for an international oil company.
 | 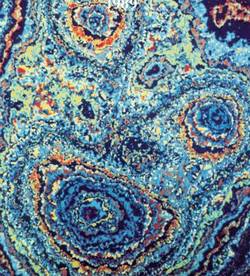 | |
| Stromatolite coll. Géologie © J.-Y. Reynaud, MNHN | Simulation of a Substitution Random Function (Chentsov covariance function, Coding based on a Markov chain with stationary uniform law) |
